排列问题（二）

#47.全排列 II

力扣题目链接(opens new window)

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：

  • 输入：nums = [1,1,2]
  • 输出： [[1,1,2], [1,2,1], [2,1,1]]

示例 2：

  • 输入：nums = [1,2,3]
  • 输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

  • 1 <= nums.length <= 8
  • -10 <= nums[i] <= 10

#思路

**如果对回溯算法基础还不了解的话，我还特意录制了一期视频：带你学透回溯算法（理论篇） (opens new window)**可以结合题解和视频一起看，希望对大家理解回溯算法有所帮助。

这道题目和46.全排列 (opens new window)的区别在与给定一个可包含重复数字的序列，要返回所有不重复的全排列。

这里又涉及到去重了。

在40.组合总和II (opens new window)、90.子集II (opens new window)我们分别详细讲解了组合问题和子集问题如何去重。

那么排列问题其实也是一样的套路。

还要强调的是去重一定要对元素进行排序，这样我们才方便通过相邻的节点来判断是否重复使用了。

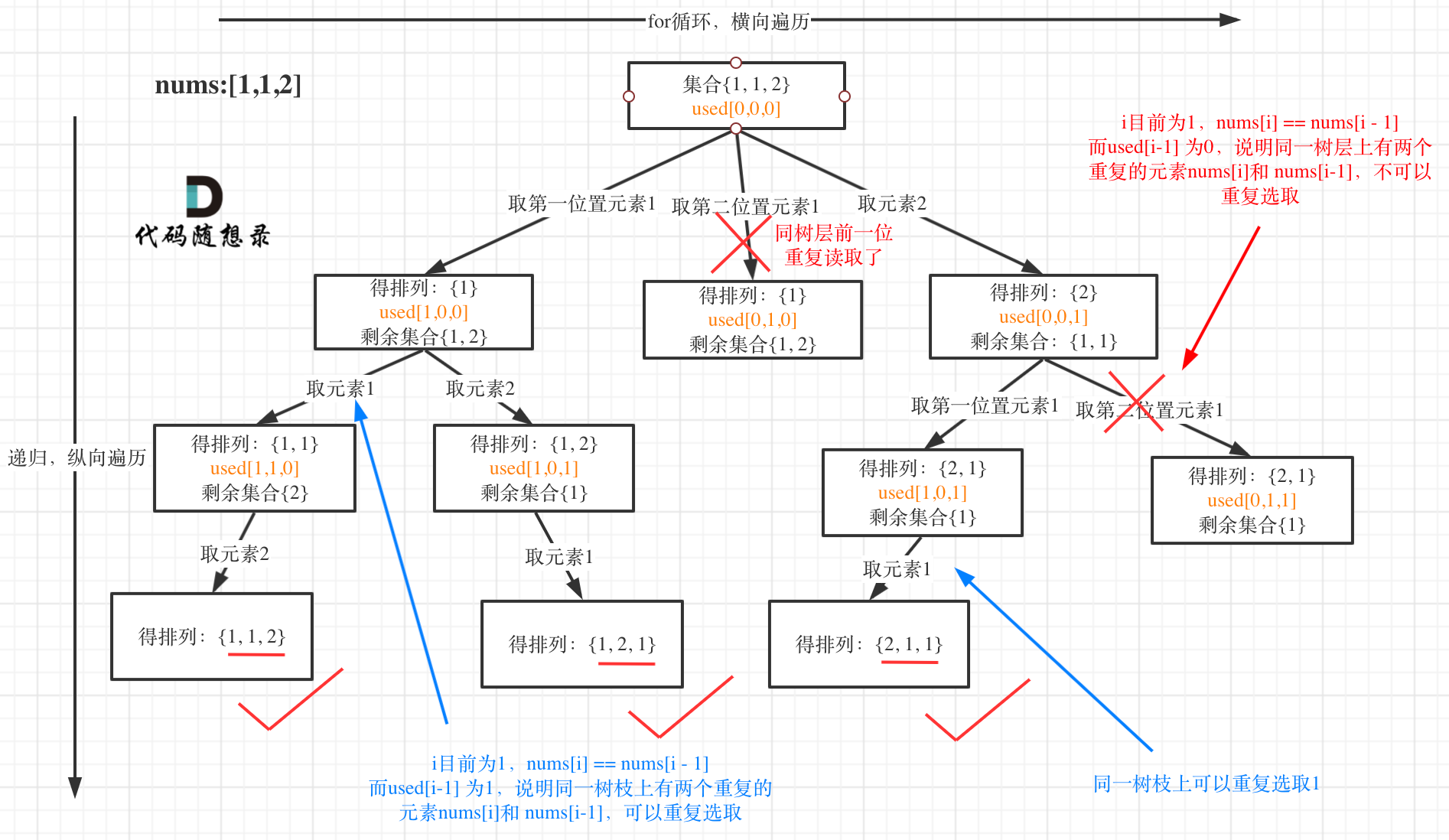
我以示例中的 [1,1,2]为例 （为了方便举例，已经排序）抽象为一棵树，去重过程如图：

47.全排列II1

图中我们对同一树层，前一位（也就是nums[i-1]）如果使用过，那么就进行去重。

一般来说：组合问题和排列问题是在树形结构的叶子节点上收集结果，而子集问题就是取树上所有节点的结果。

在46.全排列 (opens new window)中已经详解讲解了排列问题的写法，在40.组合总和II (opens new window)、90.子集II (opens new window)中详细讲解的去重的写法，所以这次我就不用回溯三部曲分析了，直接给出代码，如下：

#C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking (vector<int>& nums, vector<bool>& used) {
        // 此时说明找到了一组
        if (path.size() == nums.size()) {
            result.push_back(path);
            return;
        }
        for (int i = 0; i < nums.size(); i++) {
            // used[i - 1] == true，说明同一树枝nums[i - 1]使用过
            // used[i - 1] == false，说明同一树层nums[i - 1]使用过
            // 如果同一树层nums[i - 1]使用过则直接跳过
            if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
                continue;
            }
            if (used[i] == false) {
                used[i] = true;
                path.push_back(nums[i]);
                backtracking(nums, used);
                path.pop_back();
                used[i] = false;
            }
        }
    }
public:
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        result.clear();
        path.clear();
        sort(nums.begin(), nums.end()); // 排序
        vector<bool> used(nums.size(), false);
        backtracking(nums, used);
        return result;
    }
};

#拓展

大家发现，去重最为关键的代码为：

1
2
3
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
    continue;
}

**如果改成 used[i - 1] == true， 也是正确的!**，去重代码如下：

1
2
3
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
    continue;
}

这是为什么呢，就是上面我刚说的，如果要对树层中前一位去重，就用used[i - 1] == false，如果要对树枝前一位去重用used[i - 1] == true。

对于排列问题，树层上去重和树枝上去重，都是可以的，但是树层上去重效率更高！

这么说是不是有点抽象？

来来来，我就用输入: [1,1,1] 来举一个例子。

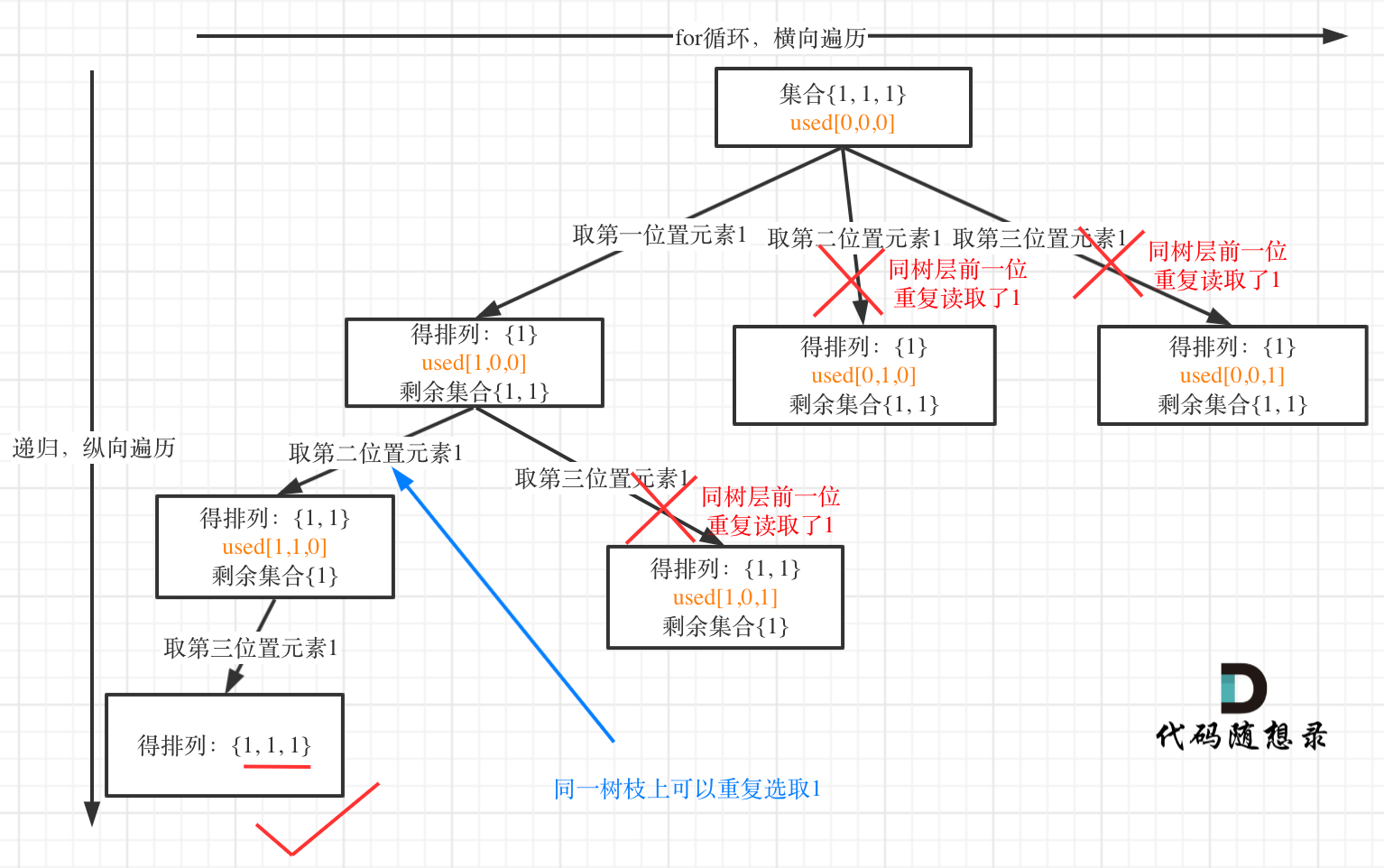
树层上去重(used[i - 1] == false)，的树形结构如下：

47.全排列II2

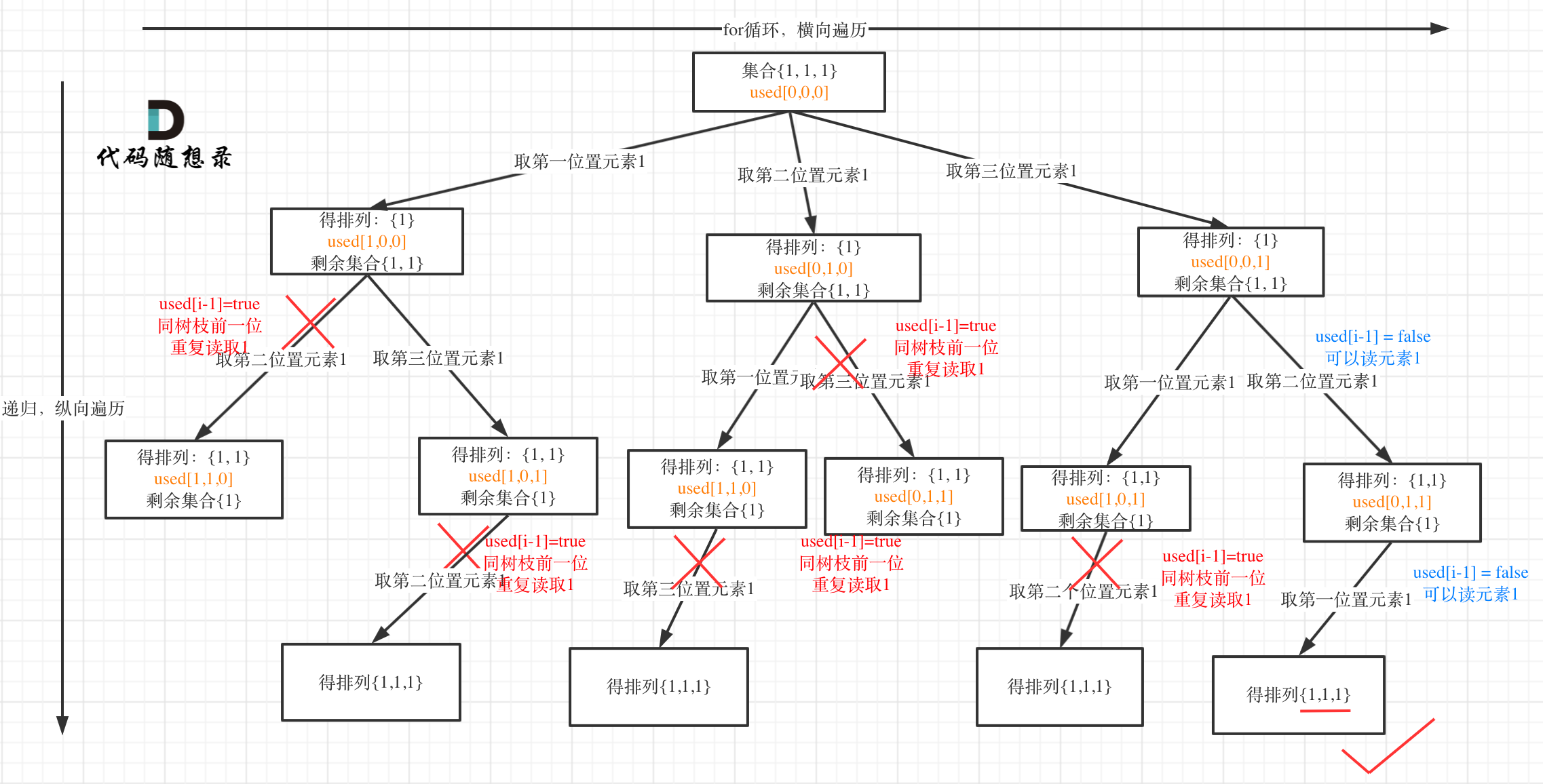
树枝上去重（used[i - 1] == true）的树型结构如下：

47.全排列II3

大家应该很清晰的看到，树层上对前一位去重非常彻底，效率很高，树枝上对前一位去重虽然最后可以得到答案，但是做了很多无用搜索

Java代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
//存放结果
  List<List<Integer>> result = new ArrayList<>();
  //暂存结果
  List<Integer> path = new ArrayList<>();

  public List<List<Integer>> permuteUnique(int[] nums) {
      boolean[] used = new boolean[nums.length];
      Arrays.sort(nums);
      backtracking(nums);
      return res;
  	
  }
  public void backtracking(int[] nums) {
  	for(int i=0;i<nums.length;i++) {
          // used[i - 1] == true，说明同⼀树⽀nums[i - 1]使⽤过
          // used[i - 1] == false，说明同⼀树层nums[i - 1]使⽤过
          // 如果同⼀树层nums[i - 1]使⽤过则直接跳过
          if(i>0 && nums[i] == nums[i-1] && used[i -1] == false) {
              continue;
          }
          if(used[i] == false) {
              used[i] = true;
              path.add(nums[i]);
          	backtracking(nums);
          	path.remove(path.size() -1);
              used[i] = false;
          }
        
      }
  }