第51题. N皇后
力扣题目链接(opens new window)
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
示例 1:

- 输入:n = 4
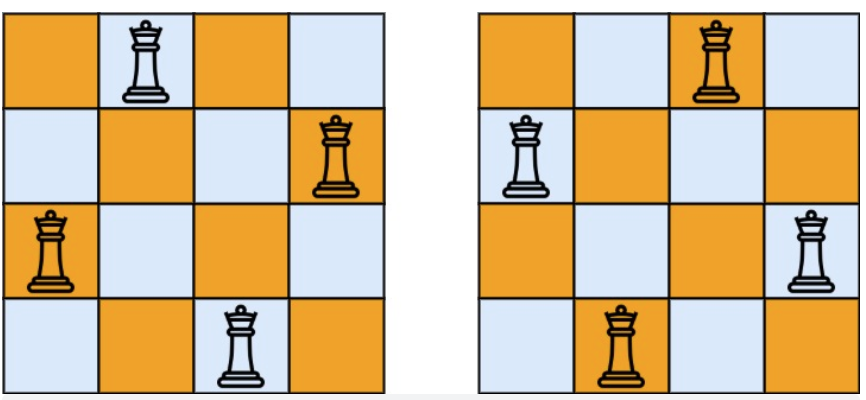
- 输出:[[“.Q..”,”…Q”,”Q…”,”..Q.”],[“..Q.”,”Q…”,”…Q”,”.Q..”]]
- 解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
**如果对回溯算法基础还不了解的话,我还特意录制了一期视频:带你学透回溯算法(理论篇) (opens new window)**可以结合题解和视频一起看,希望对大家理解回溯算法有所帮助。
都知道n皇后问题是回溯算法解决的经典问题,但是用回溯解决多了组合、切割、子集、排列问题之后,遇到这种二维矩阵还会有点不知所措。
首先来看一下皇后们的约束条件:
- 不能同行
- 不能同列
- 不能同斜线
确定完约束条件,来看看究竟要怎么去搜索皇后们的位置,其实搜索皇后的位置,可以抽象为一棵树。
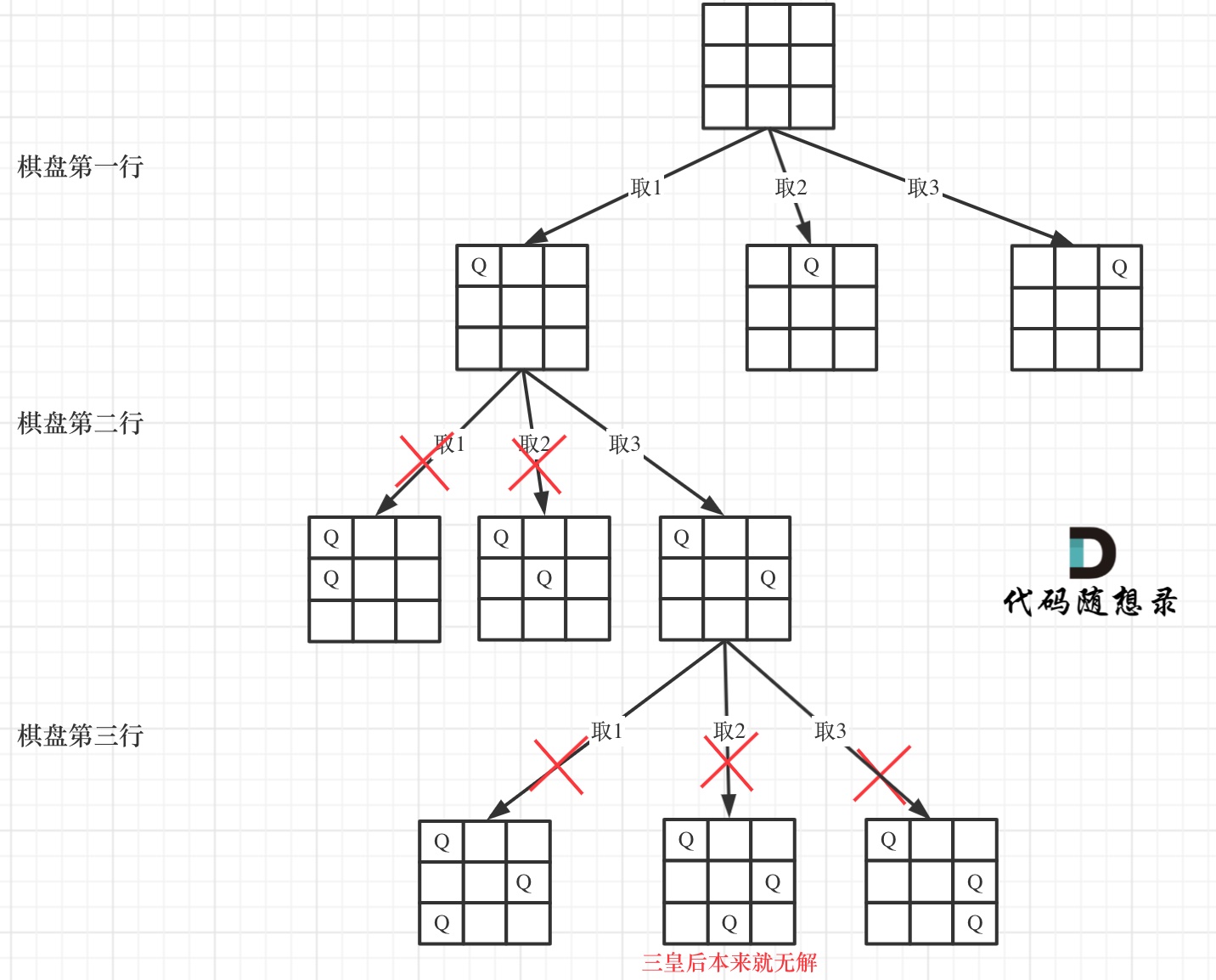
下面我用一个 3 * 3 的棋盘,将搜索过程抽象为一棵树,如图:

从图中,可以看出,二维矩阵中矩阵的高就是这棵树的高度,矩阵的宽就是树形结构中每一个节点的宽度。
那么我们用皇后们的约束条件,来回溯搜索这棵树,只要搜索到了树的叶子节点,说明就找到了皇后们的合理位置了。
#回溯三部曲
按照我总结的如下回溯模板,我们来依次分析:
1
2
3
4
5
6
7
8
9
10
11
| void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}
|
我依然是定义全局变量二维数组result来记录最终结果。
参数n是棋盘的大小,然后用row来记录当前遍历到棋盘的第几层了。
代码如下:
1
2
| vector<vector<string>> result;
void backtracking(int n, int row, vector<string>& chessboard) {
|
在如下树形结构中: 
可以看出,当递归到棋盘最底层(也就是叶子节点)的时候,就可以收集结果并返回了。
代码如下:
1
2
3
4
| if (row == n) {
result.push_back(chessboard);
return;
}
|
递归深度就是row控制棋盘的行,每一层里for循环的col控制棋盘的列,一行一列,确定了放置皇后的位置。
每次都是要从新的一行的起始位置开始搜,所以都是从0开始。
代码如下:
1
2
3
4
5
6
7
| for (int col = 0; col < n; col++) {
if (isValid(row, col, chessboard, n)) {
chessboard[row][col] = 'Q';
backtracking(n, row + 1, chessboard);
chessboard[row][col] = '.';
}
}
|
按照如下标准去重:
- 不能同行
- 不能同列
- 不能同斜线 (45度和135度角)
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| bool isValid(int row, int col, vector<string>& chessboard, int n) {
for (int i = 0; i < row; i++) {
if (chessboard[i][col] == 'Q') {
return false;
}
}
for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {
if (chessboard[i][j] == 'Q') {
return false;
}
}
for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
if (chessboard[i][j] == 'Q') {
return false;
}
}
return true;
}
|
在这份代码中,细心的同学可以发现为什么没有在同行进行检查呢?
因为在单层搜索的过程中,每一层递归,只会选for循环(也就是同一行)里的一个元素,所以不用去重了。
Java代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
| class Solution {
List<List<String>> res;
public List<List<String>> solveNQueens(int n) {
res = new ArrayList<>();
char[][] chessboard = new char[n][n];
for (char[] c : chessboard) {
Arrays.fill(c, '.');
}
backtracking(n,0,chessborad);
return res;
}
public List Array2List(char[][] chessboard) {
List<String> list = new ArrayList<>();
for (char[] c : chessboard) {
list.add(String.copyValueOf(c));
}
return list;
}
public void backtracking(int n,int row,char[][] chessboard) {
if(n == row) {
res.add(Array2List(chessborad));
return;
}
for(int col = 0;col<n;col++) {
if(isValid(row,col,chessboard)) {
chessboard[row][col] = 'Q';
backtracking(n,row + 1,chessboard);
chessboard[row][col] = '.';
}
}
}
public boolean isValid(int row,int col,char[][] chessboard) {
for(int i=0;i<row;i++) {
if(chessboard[i][col] == 'Q') return false;
}
for(int i=col,int j=row;i>=0&&j>=0;j--,i--) {
if(chessboard[j][i] == 'Q') return false;
}
for(int i=col,int j=row;i<n&&j>=0;i++,j--) {
if(chessboard[j][i] == 'Q') return false;
}
return true;
}
}
|